2013高考直线与圆_高考直线和圆选择题及解析

1.过原点的直线与圆x∧2＋y∧2－6x＋5=0相交于A,B两点，求弦AB中点M的轨迹方程。只求等量关

2.已知过点P(2,2) 的直线与圆 相切, 且与直线 垂直, 则 （ ） A． B．1 C．2 D

3.高考数学问题:过点M(3,0)作直线l与圆x^2+y^2=16交于两点

4.圆与直线公共点问题

5.若直线始终平分圆的周长,则的最小值为( )A、B、C、D、

6.高考数学圆的知识点归纳

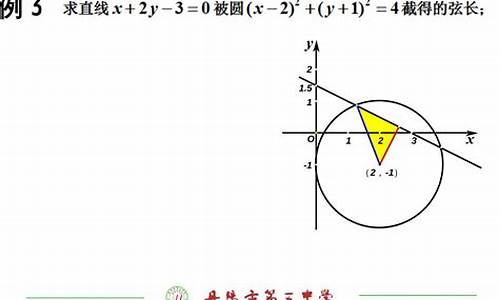
⑴直线5x+12y-13=0与圆x?+y?=1；

5x+12y-13=0 (1)

x^2+y^2=1 (2)

sub (1) into (2)

x^2 + (13-5x)^2/144 = 1

144x^2 + (13-5x)^2= 144

169x^2 -120x +25 =0

Δ = 120^2 -4(169)(25)=-2500 <0

直线5x+12y-13=0与圆x?+y?=1 不相交

//

⑵直线6x-8y+3=0与圆(x-1)?+(y-2)?=4；

6x-8y+3=0 (1)

(x-1)^2+(y-2)^2=4 (2)

sub (1) into (2)

(x-1)^2+[(1/8)(6x+3)-2]^2=4

64(x-1)^2+[(6x+3)-16]^2=256

64(x-1)^2+(6x-13)^2=256

100x^2-284x-151 =0

Δ>0

直线6x-8y+3=0与圆(x-1)?+(y-2)?=4 相交于2点

//

⑶直线x+y-4=0与圆x?+y?+2x-1=0.

x+y-4=0 (1)

x^2+y^2+2x-1=0 (2)

sub (1) into (2)

x^2+y^2+2x-1=0

x^2+(4-x)^2+2x-1=0

2x^2 -6x+15=0

Δ=(-6)^2 -4(2)(15) = -84 <0

直线x+y-4=0与圆x?+y?+2x-1=0 没有相交

过原点的直线与圆x∧2＋y∧2－6x＋5=0相交于A,B两点，求弦AB中点M的轨迹方程。只求等量关

（1） ；（2）

试题分析：（1）联立方程组 化简得 ， 故 ， （2）所求圆的圆心为AB中点 ,所求面积最小的圆的方程是 点评：圆的方程、直线与圆的位置关系，圆的切线问题与弦长问题都是高考中的热点问题；求圆的方程或找圆心坐标和半径的常用方法是待定系数法及配方法，应熟练掌握，还应注意恰当运用平面几何知识以简化计算

已知过点P(2,2) 的直线与圆 相切, 且与直线 垂直, 则 （ ） A． B．1 C．2 D

解：（图像辅助）

圆C：(x-3)^2+y^2=4

则圆心 C(3,0)，因为M是弦AB的中点

所以CM⊥OC

在直角△OMC中，斜边OC的中点设为P(3/2,0)

那么|PM|=1/2|OC|=|OP|=3/2

即M的轨迹为到定点P(3/2,0)的距离等于定长3/2的曲线

所以M的轨迹为P（3/2,0）为圆心，r=3/2为半径的圆

所以M轨迹方程为：(x-3/2)^2+y^2=9/4

且M必须在圆C内部，所以定义域为：｛x|1<x<5}

满意请采纳哦，谢谢！！

高考数学问题:过点M(3,0)作直线l与圆x^2+y^2=16交于两点

C

由题意可设切线方程为 ,又因为切线过点P(2,2)，所以 ，即切线方程为 ，所以 ，解得 ，故选C. 考点定位本小题主要考查直线方程、两条直线的位置关系、直线与圆的位置关系等基础知识，直线与圆一直是文科数学高考的一个热点，熟练其基本知识是解答好这类题目的关键.

圆与直线公共点问题

1.选C

S(AOB)=1/2?OA?OB?sin∠AOB

OA=OB=4所以要使面积最大即∠AOB=90°

OA⊥OB

设A、B坐标为(x1,y1)(x2,y2)

直线方程为y=k(x-3)

则:x1x2+y1y2=0

化简得：

（1+k^2）x1x2+9k^2-3k^2(x1+x2)=0

由直线和圆相交得：

（1+k^2）x^2-6k^2x+9k^2-16=0

变换后得：

k^2=8

2.A

曲线{x=(m+1)/(m+2),y=2m/(m+2)}可化简为

4x-y-2=0

不相交只要平行即可

所以斜率也为4

3.题的答案就是k<-2/5或k>1/10

解析如下：

y^2=x-5?(y>0)?y=kx+2

有图像可知：

下面的直线斜率为-2/5?只要满足k<-2/5成立

上面的直线斜率求解如下：

ky^2-y+2+5k=0

△=0?可求解?k=1/10?k=-1/2?(排除由图像可知k>0)

所以k>1/10成立

若直线始终平分圆的周长,则的最小值为( )A、B、C、D、

呵呵又是你的问题。

我是这样考虑的：

x^2+y^2=50的整数解为：

x=正负1 y=正负7

x=正负5 y=正负5

x=正负7 y=正负1

这些就是圆上横纵坐标都为整数的点，总共有12个这样的点（每组解就是四个点）。

直线方程中ab均不为零，所以这条直线既不与x轴平行也不与y轴平行，而且不经过原点。

圆上12个点，每两点连成一条直线，可以连C12 2(排列组合)=66条，再加上12个点上的12条切线，总共66+12＝78条。

再减去和坐标轴平行的12条以及过原点的6条，剩下符合条件的60条。

不知道我这样能否说明白，要画个图就好理解了。

祝你高考顺利。

高考数学圆的知识点归纳

本题考查的是直线与圆性质及其综合应用,由已知条件我们可以判定直线必过圆的圆心,则不难求出表示的点在平面直线直角坐标系中的位置,分析表达式的几何意义,找出满足条件的点的坐标,即可求出答案.

解:直线始终平分圆的周长

直线必过圆的圆心

即圆心点在直线上

则

则表示点至直线点的距离的平方

则其最小值

故选

直线的性质与圆的方程都是高考必须要考的知识点,此题巧妙地将直线与圆性质融合在一起进行考查,题目有一定的思维含量但计算量不大,所以题型设置为选择题,该试题立足基础考查了学生思维能力与运算能力以及灵活运用所学数学知识处理相关问题的能力,有一定的选拔作用同时对中学数学教学具有产生较好地导向作用.

在同一平面内，到一个定点的距离都相等的点组成的图形。下面是我为大家整理的关于高考数学圆的知识点归纳，希望对您有所帮助。欢迎大家阅读参考学习!

目录

圆知识点归纳：圆的定义。

圆知识点归纳：圆的各元素。

圆知识点归纳：圆的基本性质。

圆知识点归纳： 圆的定义。

1、以定点为圆心，定长为半径的点组成的图形。

2、在同一平面内，到一个定点的距离都相等的点组成的图形。

〈〈〈

圆知识点归纳： 圆的各元素。

1、半径：圆上一点与圆心的连线段。

2、直径：连接圆上两点有经过圆心的线段。

3、弦：连接圆上两点线段(直径也是弦)。

4、弧：圆上两点之间的曲线部分。半圆周也是弧。

(1)劣弧：小于半圆周的弧。

(2)优弧：大于半圆周的弧。

5、圆心角：以圆心为顶点，半径为角的边。

6、圆周角：顶点在圆周上，圆周角的两边是弦。

7、弦心距：圆心到弦的垂线段的长。

〈〈〈

圆知识点归纳： 圆的基本性质。

1、圆的对称性。

(1)圆是轴对称图形，它的对称轴是直径所在的直线。

(2)圆是中心对称图形，它的对称中心是圆心。

(3)圆是旋转对称图形。

2、垂径定理。

(1)垂直于弦的直径平分这条弦，且平分这条弦所对的两条弧。

(2)推论：

平分弦(非直径)的直径，垂直于弦且平分弦所对的两条弧。

平分弧的直径，垂直平分弧所对的弦。

3、圆心角的度数等于它所对弧的度数。圆周角的度数等于它所对弧度数的一半。

(1)同弧所对的圆周角相等。

(2)直径所对的圆周角是直角;圆周角为直角，它所对的弦是直径。

4、在同圆或等圆中，两条弦、两条弧、两个圆周角、两个圆心角、两条弦心距五对量中只要有一对量相等，其余四对量也分别相等。

5、夹在平行线间的两条弧相等。

6、设⊙O的半径为r，OP=d。

7、(1)过两点的圆的圆心一定在两点间连线段的中垂线上。

(2)不在同一直线上的三点确定一个圆，圆心是三边中垂线的交点，它到三个点的距离相等。

(直角三角形的外心就是斜边的中点。)

8、直线与圆的位置关系。d表示圆心到直线的距离，r表示圆的半径。

直线与圆有两个交点，直线与圆相交;直线与圆只有一个交点，直线与圆相切;

直线与圆没有交点，直线与圆相离。

9、平面直角坐标系中，A(x1，y1)、B(x2，y2)。则AB=

10、圆的切线判定。

(1)d=r时，直线是圆的切线。

切点不明确：画垂直，证半径。

(2)经过半径的外端且与半径垂直的直线是圆的切线。

切点明确：连半径，证垂直。

11、圆的切线的性质(补充)。

(1)经过切点的直径一定垂直于切线。

(2)经过切点并且垂直于这条切线的直线一定经过圆心。

12、切线长定理。

(1)切线长：从圆外一点引圆的两条切线，切点与这点之间连线段的长叫这个点到圆的切线长。

(2)切线长定理。

∵ PA、PB切⊙O于点 A、B

PA=PB，2。

13、内切圆及有关计算。

(1)三角形内切圆的圆心是三个内角平分线的交点，它到三边的距离相等。

(2)如图，△ABC中，AB=5，BC=6，AC=7，⊙O切△ABC三边于点D、E、F。

求：AD、BE、CF的长。

分析：设AD=x，则AD=AF=x，BD=BE=5-x，CE=CF=7-x.

可得方程：5-x+7-x=6，解得x=3

(3)△ABC中，C=90，AC=b，BC=a，AB=c。

求内切圆的半径r。

分析：先证得正方形ODCE，

得CD=CE=r

AD=AF=b-r，BE=BF=a-r

b-r+a-r=c

得r=

(4)S△ABC=

14、(补充)

(1)弦切角：角的顶点在圆周上，角的一边是圆的切线，另一边是圆的弦。

如图，BC切⊙O于点B，AB为弦，ABC叫弦切角，ABC=D。

(2)相交弦定理。

圆的两条弦AB与CD相交于点P，则PAPB=PCPD。

(3)切割线定理。

如图，PA切⊙O于点A，PBC是⊙O的割线，则PA2=PBPC。

(4)推论：如图，PAB、PCD是⊙O的割线，则PAPB=PCPD。

15、圆与圆的位置关系。

(1)外离：dr1+r2， 交点有0个;

外切：d=r1+r2， 交点有1个;

相交：r1-r2

内切：d=r1-r2， 交点有1个;

内含：0d

(2)性质。

相交两圆的连心线垂直平分公共弦。

相切两圆的连心线必经过切点。

16、圆中有关量的计算。

(1)弧长有L表示，圆心角用n表示，圆的半径用R表示。

L=

(2)扇形的面积用S表示。

S= S=+

(3)圆锥的侧面展开图是扇形。

r为底面圆的半径，a为母线长。

扇形的圆心角=

S侧= ar S全= ar+ r2

〈〈〈

高考数学圆的知识点归纳相关 文章 ：

★ 高考数学圆的知识点归纳

★ 高考数学必考知识点考点大全总结

★ 高考数学知识点归纳总结

★ 高考数学知识点归纳总结

★ 高考数学知识点归纳整理

★ 高考数学必考知识点归纳

★ 高考数学知识点总结大全

★ 高中数学必考知识点归纳整理

★ 高三数学知识点总结归纳

★ 高三数学知识点考点总结大全

var _hmt = _hmt || []; (function() { var hm = document.createElement("script"); hm.src = ""; var s = document.getElementsByTagName("script")[0]; s.parentNode.insertBefore(hm, s); })();