高考立体几何向量,高考立体几何向量法好还是几何法好

1.高考数学立体几何大题都可以用向量法吗？

2.立体几何，用空间向量解答。并求解释一下用空间向量解答线线距离，线面距离，点面距离，线面角的基本方法

3.高考立体几何都能用向量法吗

4.高中几何向量运算公式

5.高考数学问题，如何用空间向量求立体几何中的二面角的正切值

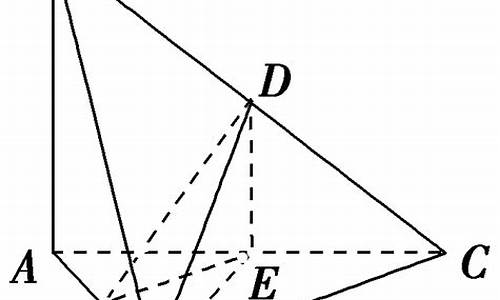
面面垂直

说明：b⊥L不一定成立。如图，设直线a对应AB，则直线b对应BF或者BE都可以满足条件。而直线L则是对应CD。由此可知b⊥L不一定成立。

证明α垂直于β实际上就是定理“如果一个平面经过了另一个平面的一条垂线，那么这两个平面互相垂直”的证明。

证明：（法向量证明）

? ∵AB⊥β

?∴向量AB即可作为β的法向量，而且AB垂直于β内任意的一条直线

? 在平面β内过B点作直线BE⊥CD

?∵AB垂直于β内任意的一条直线

?∴AB⊥BE

?∵AB与CD交于B点

?∴BE⊥α

∴向量BE即可作为的α法向量

?又∵向量AB即可作为β的法向量，且AB⊥BE

?∴α⊥β

(二面角证明)

? ∵AB⊥β

?∴AB垂直于β内任意的一条直线

?∴AB⊥CD.

?在平面β内过B点作直线BE⊥CD，则∠ABE就是二面角α--CD--β的平面角

?又∵AB垂直于β内任意的一条直线

?∴AB⊥BE

?∴二面角α--CD--β是直二面角

?∴α⊥β

高考数学立体几何大题都可以用向量法吗？

线面角?

向量n，向量a为线的向量，则cos=(向量a*向量n）/(向量a的模*向量n的模）

面面角?

向量n1，向量,2，则；cos=(向量n1*向量n2）/(向量n1的模*向量n2的模）

点到线的距离公式(点到线的距离公式属于平面直角坐标系中的知识）

设P(X,Y)直线L：ax+by+c=0,则点P到线L的距离：(aX+bY+c)/根号下（a^2+b^2）

扩展资料：

1、共线向量定理

两个空间向量a,b向量(b向量不等于0），a∥b的充要条件是存在唯一的实数λ，使a=λb

2、共面向量定理

如果两个向量a,b不共线，则向量c与向量a,b共面的充要条件是：存在唯一的一对实数x,y,使c=ax+by

3、空间向量分解定理

如果三个向量a、b、c不共面，那么对空间任一向量p，存在一个唯一的有序实数组x，y，z，使p=xa+yb+zc。

任意不共面的三个向量都可作为空间的一个基底，零向量的表示唯一。

立体几何，用空间向量解答。并求解释一下用空间向量解答线线距离，线面距离，点面距离，线面角的基本方法

高考立体几何基本都可建系，向量法肯定没问题，几何法一般只在那种很简单，很显而易见的时候用，如果两分钟内还想不出几何法，那就用向量法吧，那不需要动脑筋，而且基本上是10以内加减法。对于几何法，关键是辅助线的作法，常用辅助线是中位线、垂线、中线，还有就是一些常用方法，如，等体积法之类的……总之几何法这东西，掌握得好做起题来会很有成就感，但关键是要找感觉，如果你离高考仅80天的话，建议你好好练好向量法吧，练好这招足够你应付高考了~~

加油！！！

高考立体几何都能用向量法吗

在矩形ABCD中，AD=4,AB=2,E,F分别是线段AB，BC的中点，PA垂直平面ABCD，三棱锥P-ABD的体积等于4，线段AD上是否存在点G，使得EG垂直PF？若存在，求出点G到平面PDF的距离。

解析：∵矩形ABCD中，AD=4,AB=2，PA⊥面ABCD

建立以A为原点，以AD方向为X轴，以AByytm为Y轴，以AP方向为Z轴正方向的空间直角坐标系A-xyz

∵三棱锥P-ABD的体积等于4

V=1/3*1/2*AD*AB*PA=1/6*4*2*PA=4==>PA=3

∵E,F分别是线段AB，BC的中点

∴点坐标：

A(0,0,0)，B(0,2,0)，C(4,2,0)，D(4,0,0)，E(0,1,0)，F(2,2,0)，P(0,0,3)

设G(x,0,0)?（0<x<4）

向量EG=(x,-1,0)，向量PF=(2,2,-3)

向量EG·向量PF=2x-2+0=0==>x=1

∴G(1,0,0)

向量PG=(1,0,-3)，向量PD=(4,0,-3)，向量PF=(2,2,-3)

设向量n(x,y,z)是面PDF的一个法向量

则向量n·向量PD=4x-3z=0；向量n·向量PF=2x+2y-3z=0

令y=1，则x=1,z=4/3

∴向量n=(1,1,4/3)==>|向量n|=√34/3

向量PG=(1,0,-3)

G到平面PDF的距离为向量PG在平面法线上的投影

即，d=|向量n·向量PG|/|向量n|

|向量n·向量PG|=|1-4|=3

∴d=3/(√34/3)=9/√34

解题的基本方法：

(1)在立体几何图形中，选择适当的点和直线方向建立空间直角坐标系中

(2)若问题中没有给出坐标计算单位，可选择合适的线段设置长度单位；

(3)计算有关点的坐标值，求出相关向量的坐标；

(4)求解给定问题

求解异面直线间距离；

求异面直线间距离的关键是根据题目给定条件寻找二条异面直线间距离所在；

点到平面距离问题；

直线与平面间距离

从直线上任取一点，求该点到平面的距离；

直线与平面夹角；

(1)求直线与平面夹角的基本方法是寻找或作直线在该平面内的射影，然后找出在直线和射影上的二个向量，进而求出其夹角。

(2)求平面的一个法向量，然后求出直线与法向量的夹角，该夹角与直线和平面夹角互余

高中几何向量运算公式

完全可以的，前年高三复习做了好多模拟卷啊真题啊，基本上都可以用向量法的，而且答案里一半立体几何都有两组答案，就是普通法和向量法，也有少数题目无法建立坐标系的，但高考真题几乎没有。只不过向量法有时不是最简单的，有的时候向量法找到合适的原点见坐标系难过直接法，比如2009年的江西高考题要反过建系还是有一定难度的。所以最好还是两种方法都会就好了，什么都不怕了

高考数学问题，如何用空间向量求立体几何中的二面角的正切值

设 → →

a =(x1,y1) b =(x2,y2)

则 a向量与b向量的夹角为：

cos＜a,b＞==[(x1,y1)·(x2,y2)] /[√(x1?＋y1?)·√(x2?+y2?)]

==(x1x2+y1y2) /[√(x1?＋y1?)·√(x2?+y2?)]

a向量与b向量的距离为

d=√[(x2-x1)?+(y2-y1)?].

答：1、如果知道这两个平面的法向量，就用这两个平面的法向量的点积除以两个法向量的模的积；得出两个法向量的余弦值。这个余弦值是两个平面角的负余弦值；如果平面角为a，这个余弦值就是cos（180D-a）=-cosa。sina=√(1-cos^2a)(是正数-算数根)；正切值：tana=sina/-cosa。

2、在不知道平面的法向量的条件，下找出两个平面的每一个平面的任意两条边（同一平面内的两条边只要是不相互垂直就可以）；做出每条边的向量，同一平面内的两条向量的叉积就是这个平面的法向量（注意如果无法判断两面角是锐角还是钝角，按照右手系使法向量指向平面角的内部方向）；然后求两个法向量的余弦值；其它同1。