您现在的位置是: 首页 > 教育改革 教育改革
高考数学三角函数题_高考三角函数难题
tamoadmin 2024-06-09 人已围观
简介1.一道向量与三角函数结合的难题2.高中三角函数难题,重金求才(1)一次齐次时,分子分母同时除以cosa,就行了。 (2)因为(cosa)^2+(sina)^2=1 这个题是二次齐次式,整体除以(cosa)^2+(sina)^2 得[2(sina)^2-3sinacosa-2(cosa)^2]/[(cosa)^2+(sina)^2] 分子分母同时除以(cosa)^2 得[2(tana)^2...一
1.一道向量与三角函数结合的难题
2.高中三角函数难题,重金求才
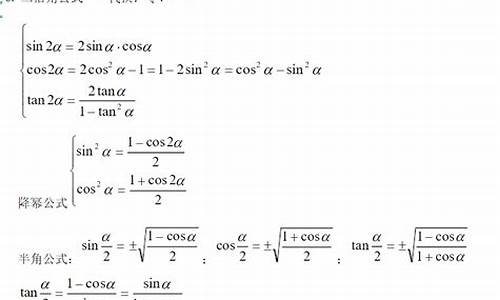
(1)一次齐次时,分子分母同时除以cosa,就行了。 (2)因为(cosa)^2+(sina)^2=1 这个题是二次齐次式,整体除以(cosa)^2+(sina)^2 得[2(sina)^2-3sinacosa-2(cosa)^2]/[(cosa)^2+(sina)^2] 分子分母同时除以(cosa)^2 得[2(tana)^2...
一道向量与三角函数结合的难题
P为锐角三角形ABC内任一点,直线AP,BP,CP分别分别交三角形PBC,PCA,PAB的外接圆于另一点A1,B1,C1(不同于P),求证:
(1+2*PA/PA1)*(1+2*PB/PB1)*(1+2*PC/PC1)>=8
高中三角函数难题,重金求才
an=(cos nπ/7,sin nπ/7)
则a?n= cos ?nπ/7+sin? nπ/7=1,
ㄧbㄧ=1,
则b?=1.
y=ㄧa1+bㄧ?+ㄧa2+bㄧ?+ㄧa3+bㄧ?++ㄧa141+bㄧ?
=a?1+2a1b+ b?+ a?2+2a2b+ b?++ a?141+2a141b+ b?
=1+2a1b+1+1+2a2b+1+1+2a141b+1
=282+2(a1+a2+……+a141)b
cosπ/7+ cos2π/7+ cos2π/7+ cos2π/7+……+ cos7π/7+
cos8π/7+ cos9π/7+ cos10π/7+ cos11π/7+……+ cos14π/7
= cosπ/7+ cos2π/7+ cos2π/7+ cos2π/7+……+ cos7π/7
-cosπ/7-cos2π/7- cos3π/7- cos4π/7+……- cos7π/7
=0,
sinπ/7+ sin2π/7+ sin2π/7+ sin2π/7+……+ sin7π/7+
sin8π/7+ sin9π/7+ sin10π/7+ sin11π/7+……+ sin14π/7
= sinπ/7+ sin2π/7+ sin2π/7+ sin2π/7+……+ sin7π/7
-sinπ/7-sin2π/7- sin3π/7- sin4π/7+……- sin7π/7
=0,
因为cos nπ/7与sin nπ/7的周期都是14,
所以a1+a2+……+a141=a1
(a1+a2+……+a141)b=a1b≤|a1||b|=1
∴y=282+2(a1+a2+……+a141)b
≤282+2=284.
题目错了一点地方!
应该是y=16-12cos?A-4cos?C ?(因为这里的自变量不是x)
解:
由根号3 cosA -cosC=1有3cos?A=(1+cosC)?
代入有:
y=16-4(1+cosC)? -4cos?C
=-8cos?C - 8cosC +12 ?, -8cosC∈(16-8根号3 ,16),故cosC∈(-4,根号3 -2)
令cosC=t,则t∈(-4,根号3 -2);
所以,
y=-8t? -8t +12 ,?t∈(-4,根号3 -2)
开口向下,对称轴为x= -1/2的抛物线在(-4,根号3 -2)的图像;
所以,y∈(-84,14为所求的值域!