您现在的位置是: 首页 > 教育改革 教育改革
柯西不等式与高考,柯西不等式 高考
tamoadmin 2024-05-19 人已围观
简介内容如下:1、二维形式:(a^2+b^2)(c^2 + d^2)(ac+bd)^2。2、三角形式:(a^2+b^2)+(c^2+d^2)[(a-c)^2+(b-d)^2]。3、向量形式:|α||β||α·β|,α=(a1,a2,…,an),β=(b1,b2,…,bn)(n∈N,n2)。4、一般形式:(∑ai^2)(∑bi^2) (∑ai·bi)^2。常用定理:①不等式F(x)< G(x)与
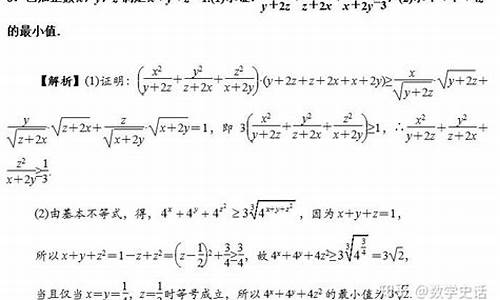
内容如下:
1、二维形式:(a^2+b^2)(c^2 + d^2)≥(ac+bd)^2。
2、三角形式:√(a^2+b^2)+√(c^2+d^2)≥√[(a-c)^2+(b-d)^2]。
3、向量形式:|α||β|≥|α·β|,α=(a1,a2,…,an),β=(b1,b2,…,bn)(n∈N,n≥2)。
4、一般形式:(∑ai^2)(∑bi^2) ≥ (∑ai·bi)^2。
常用定理:
①不等式F(x)< G(x)与不等式 G(x)>F(x)同解。
②如果不等式F(x) < G(x)的定义域被解析式H( x )的定义域所包含,那么不等式 F(x)<G(x)与不等式F(x)+H(x)<G(x)+H(x)同解。
③如果不等式F(x)<G(x) 的定义域被解析式H(x)的定义域所包含,并且H(x)>0,那么不等式F(x)<G(x)与不等式H(x)F(x)<H( x )G(x) 同解。
④不等式F(x)G(x)>0与不等式同解;不等式F(x)G(x)<0与不等式同解。
caucy 不等式还是记一下为好,排序不等式不会考的。这些东西都是一个数学技巧,高考讲究的考察大纲,所以不会出现那样的偏题。但是掌握了还是有好处的啊。学数学吗,重在自己喜欢。不能为了考试而去学了。。。。