高考数学之圆锥曲线专题_江苏高考圆锥曲线

1.圆锥曲线弦长五大秒杀公式是什么？

2.江苏高考，数学，第15题，第16题，第17题，第18题，第19题，第20题。题目的内容分别包括哪些知识点。

3.谁能告诉我江苏高考数学圆锥曲线中 双曲线和抛物线 有没有可能考解答题呢？

4.高考数学圆锥曲线积分怎么做?

5.圆锥曲线在高考中的占比

6.圆锥曲线定点定值问题方法总结

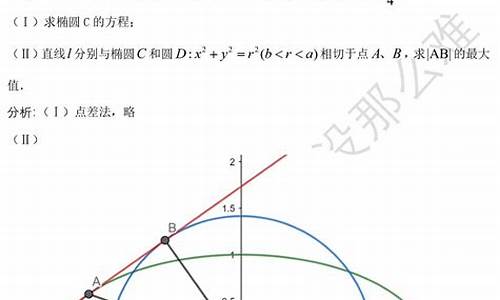
2023江苏高考数学试卷难吗介绍如下：

江苏高考数学试卷总体来说难度加大,部分考完高考数学的考生表示,数学题很难,从近几年的高考试卷难度来看,总体上难度呈现上升。

高考数学时间分配原则

对于高考数学基础比较薄弱的同学，重在保简易题。鉴于高考数学客观题部分主要是对基础知识点的考察，可以稍稍放慢速度，把时间控制在50-60分钟，力求做到准确细致，尽量保证70分的基础分不丢分。

之后的三道简易高考数学解答题每题平均花10-15分钟完成。至于后三道高考数学大题，建议先阅读完题目，根据题意把可以联想到的常考知识点写出来，例如涉及函数单调性、切线斜率的可对函数求导，圆锥曲线的设出标准方程、数列里求出首项等等。如果没有其它的思路，不要耽误太多时间，把剩下的时间倒回去检查前面的题目。

高考数学题要认真仔细对于一道具体的习题，解题时最重要的环节是审题。审题的第一步是读题，这是获取信息量和思考的过程。所以，在高考数学实际解题时，应特别注意，审题要认真、仔细。

圆锥曲线弦长五大秒杀公式是什么？

在每年的高考中,有关圆锥曲线的试题约占全卷总分的13%，是相当重要的考点。下面我整理了《高中数学圆锥曲线公式大全》，欢迎阅读。

　高中数学圆锥曲线公式大全

1.焦半径公式 ，P为椭圆上任意一点，则│PF1│= a + eXo

│PF2│= a - eXo

F1 F2分别为其左，右焦点

2.通径长 = 2b?/a

3.焦点三角形面积公式

S⊿PF1F2 = b?tanθ/2 θ为∠F1PF2

这个可能有点难理解，不过结合第一定义可以较快的推，双曲线的也是同样方法

4.左准点Q 自己取的名字方便叙述，准线与X轴的焦点

过左焦点F1的任意一条线与椭圆交与A ，B 那么一定有：X轴平分∠AQB

在右边也是一样

1.通径就不说了 2.焦半径公式有8个，很难打符号的，不过可以根据极座标方程来直接解答，比焦半径公式还快一些

3.焦点三角形面积公式

S⊿PF1F2 =b?cotθ/2 左右支都是它

y?=2px p>0过焦点的直线交它于AX1,Y1,BX2,Y2两点

1.│AB│=X1 + X2 + p =2p/sin?θ θ为直线AB的倾斜角

2. Y1*Y2 = -p? ， X1*X2 = p?/4

3.1/│FA│ + 1/│FB│ = 2/p

4.结论：以AB 为直径的圆与抛物线的准线线切

5.焦半径公式： │FA│= X1 + p/2 = p/1-cosθ

直线与圆锥曲线 y= Fx 相交于A ，B，则

│AB│=√1+k? * [√Δ/│a│]

圆锥曲线包括椭圆圆为椭圆的特例，抛物线，双曲线。

圆锥曲线二次曲线的统一定义：

到定点焦点的距离与到定直线准线的距离的商是常数e离心率的点的轨迹。当e>1时，为双曲线的一支，当e=1时，为抛物线，当0

有途网我建议还是先研究书本的基本概念，掌握相关公式，图形特点，利用这些概念解决题目，之后再做习题。

高中数学主要考点及易错点整理

高中数学易错点

不等式

1.利用均值不等式求最值时，你是否注意到：“一正;二定;三等”.

2.绝对值不等式的解法及其几何意义是什么?

3.解分式不等式应注意什么问题?用“根轴法”解整式分式不等式的注意事项是什么?

4.解含引数不等式的通法是“定义域为前提，函式的单调性为基础，分类讨论是关键”，注意解完之后要写上：“综上，原不等式的解集是……”.

5.在求不等式的解集、定义域及值域时，其结果一定要用 *** 或区间表示;不能用不等式表示.

6.两个不等式相乘时,必须注意同向同正时才能相乘,即同向同正可乘;同时要注意“同号可倒”即a>b>0，a<0.

　高中数学易错点

数列

1.解决一些等比数列的前项和问题，你注意到要对公比及两种情况进行讨论了吗?

2.在“已知，求”的问题中,你在利用公式时注意到了吗?时，应有需要验证，有些题目通项是分段函式。

3.你知道存在的条件吗?你理解数列、有穷数列、无穷数列的概念吗?你知道无穷数列的前项和与所有项的和的不同吗?什么样的无穷等比数列的所有项的和必定存在?

4.数列单调性问题能否等同于对应函式的单调性问题?数列是特殊函式，但其定义域中的值不是连续的。

5.应用数学归纳法一要注意步骤齐全，二要注意从到过程中，先假设时成立，再结合一些数学方法用来证明时也成立。

高中数学主要考点：立体几何初步

考点1：空间几何体的结构、三检视和直检视

考点2：空间几何体的表面积和体积

考点3：点、线、面的位置关系

考点4：直线、平面平行的性质与判定

考点5：直线、平面垂直的判定及其性质

高中数学主要考点：三角函式

考点1：任意角的三角函式、同三角函式和诱导公式

考点2：三角函式的影象和性质

考点3：三角函式的最值与综合运用

考点4：三角恒等变换

考点5：解三角形

高中数学主要考点：数列

考点1：数列的概念及其表示

考点2：等差数列

考点3:等比数列

考点4：数列的综合运用

江苏高考，数学，第15题，第16题，第17题，第18题，第19题，第20题。题目的内容分别包括哪些知识点。

圆锥曲线公式：

一、椭圆

1、中心在原点，焦点在x轴上的椭圆标准方程：其中x?/a?+y?/b?=1,其中a>b>0,c?=a?-b?。

2、中心在原点，焦点在y轴上的椭圆标准方程：y?/a?+x?/b?=1,其中a>b>0,c?=a?-b?。

参数方程：x=acosθ;y=bsinθ(θ为参数，0≤θ≤2π)

二、双曲线

1、中心在原点，焦点在x轴上的双曲线标准方程：x?/a-y?/b?=1,其中a>0，b>0，c?=a?+b?。

2、中心在原点，焦点在y轴上的双曲线标准方程：y?/a?-x?/b?=1,其中a>0，b>0，c?=a?+b?。

参数方程：x=asecθ;y=btanθ(θ为参数)

三、抛物线

参数方程:x=2pt?；y=2pt(t为参数)t=1/tanθ(tanθ为曲线上点与坐标原点确定直线的斜率)特别地，t可等于0。

直角坐标:y=ax?+bx+c(开口方向为y轴，a≠0)x=ay?+by+c(开口方向为x轴，a≠0)。

四、离心率

椭圆，双曲线，抛物线这些圆锥曲线有统一的定义：平面上，到定点的距离与到定直线的距离的比e是常数的点的轨迹叫做圆锥曲线。且当0<e<1时为椭圆：当e=1时为抛物线;当e>1时为双曲线。

如何秒杀高考圆锥曲线大题？

根据题设的已知条件，利用待定系数法列出二元二次方程，求出椭圆的方程，并化为标准方程。

直线设为斜截式y=kx+m，将直线与椭圆联立得到如图一元二次方程。注意该式子具有普适性，由笔者根据硬解定理简化而来。

通常要验证判别式大于零（因为无论是该经验所给的弦长公式还是韦达定理都是在判别式大于零的情况下才有意义，若题目给出直线与椭圆相交则略去该步，多写不扣分）。

直接写出需要的弦长公式或韦达定理。该图可以省去你至少5分钟，而且不会算错，因为你根本就不用算。

恒成立问题的证明可能会与导数，不等式交汇。恒成立问题的证伪只要找到反例即可。存在性问题通常是存在的，方法是提出无关的未知数。

谁能告诉我江苏高考数学圆锥曲线中 双曲线和抛物线 有没有可能考解答题呢？

15．（本小题满分14分）

在 中，已知 ．

（1）求证： ；

（2）若 求A的值．

16．（本小题满分14分）

F

如图，在直三棱柱 中， ， 分别是棱 上的点（点D 不同于点C），且 为 的中点．

E

求证：（1）平面 平面 ；[来源:学§科§网]

（2）直线 平面ADE．

（第16题）

D

C

A

B

17．（本小题满分14分）

如图，建立平面直角坐标系xOy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程 表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．

（1）求炮的最大射程；

（2）设在 第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标a不超过多少时，炮弹可以击中它？请说明理由．[来源:学+科+网Z+X+X+K][来源:Zxxk.Com]

x（千米）

y（千米）

O

（第17题）

18．（本小题满分16分 ）

已知a，b是实数，1和 是函数 的两个极值点．

（1）求a和b的值；

（2）设函数 的导函数 ，求 的极值点；

（3）设 ，其中 ，求函数 的零点个数．

19．（本小题满分 16分）

A

B

P

O

x

y

（第19题）

如图，在平面直角坐标系x Oy中，椭圆 的左、右焦点分别为 ， ．已知 和 都在椭圆上，其中e为椭圆的离心率．

（1）求椭圆的离心率；

（2）设A，B是椭圆上位于x轴上方的两点，且直线

与直线 平行， 与 交于点P．

（i）若 ，求直线 的斜率；

（ii）求证： 是定值．

20．（本小题满分16分）

已知各项均为正数的两个数列 和 满足： ．

（1）设 ，求证：数列 是 等差数列；

（2）设 ，且 是等比数列，求 和 的值．

2012年的高考的大体形式就是这样，每年都差不多

高考数学圆锥曲线积分怎么做?

考，很可能考。

我们知道，双曲线可以是反比例函数的图像，抛物线可以是二次函数的图像，这在浙江省中考是必考的。

建议你买些关于圆锥曲线的参考资料，如王后雄教案等，然后做些习题，三年高考两年模拟，还有五年高考三年模拟都是很不错的，还有其他专项复习题等，你去书店看看，对你有一定的帮助。

望采纳。

圆锥曲线在高考中的占比

很多朋友或同学们并不懂积分。所以，在下用合理的逻辑，做简单的解释，具备初高中数学都可理解。如下：

首先给个圆柱，高H，底半径R（H与R非无穷大）。

然后，以它的底和高为基础在内部做个圆柱。

怎么比较二者体积呢？关键时刻来了

这里我们先给定几个定义，

1， 假定上帝存在；

2， 用上帝之刀平行于圆柱底均匀切割N次，使N无穷大，得到（N+1）个圆柱和圆锥的切面, 切面的厚度为H/（N+1）；

3， 无穷切, 使N无穷大到某程度，得到 Δr= R/N ,使得Δr为圆锥的元点半径（不能更小，类 似电子电荷（元电荷）电量）。这是逻辑上的关键，请深刻理解。

理解了以上定义，我们就可以知道相关计算数据了。对于圆锥的所有切面而言，

各切面半径从顶到底依次为0，Δr，2Δr，…mΔr，…NΔr=R（ 因为Δr已定义不可再分），

圆锥各切面面积从顶到底依次为0，πΔr^2,π(2Δr)^2……π（NΔr)^2，

各单切面体积依次是 切面面积*(H/(N+1))

故圆锥体积等于所有切面的体积加和

V锥=（πΔr^2）*(0+1+2^2+3^2+...+N^2) * (H/(N+1))

我们再来看看圆柱的体积。它是(N+1)个圆柱切面体积的加和，很简单

V柱=(N+1) * （πR^2）*（H/(N+1)）=(N+1) *（π（NΔr)^2）*（H/(N+1)）

故 V锥/ V柱=(0+1+2^2+3^2+...+N^2) / ((N^2)*(N+1))

根据数列知识，

V锥/ V柱=N*(N+1)*(2N+1)/6 / ((N^2)*(N+1))=1/3+1/(6 N)

故，N为无穷大时，V锥/ V柱=1/3

圆锥曲线定点定值问题方法总结

该占比在15%左右。

根据2023年考试大纲，圆锥曲线在高考中的占比通常为25-30分，在整张高考试卷中占比约为15%。

圆锥曲线是高考压轴题必考题型之一，这个考点主要考查学生对圆锥曲线的理解与掌握，包括椭圆的定义及标准方程、双曲线的定义及标准方程、抛物线的定义及标准方程等知识点。

圆锥曲线中的定点、定值问题是高考中的常考题型，难度较大，考查知识间的联系与综合，并且此类题一般计算量都较大，费时费力难以攻破，令很多学生望而生畏. 本文给出此类问题的求解方法，希望对同学们学习有所帮助.

圆锥曲线中的定点、定值问题求解有两大方法，即参数法和由特殊到一般的方法.

圆锥曲线的定点、定值问题会涉及到曲线上的动点及动直线，所以很常用的方法就是设动点或设动直线，即引入参数解决问题，那么设参数就有两种情况，第一种是设点的坐标，第二种是设直线的斜率.

用参数法解决定点和定值问题时，对参数的处理是不同的.